[R8I7]
Machine learning and statistics have been rapidly advancing in the past decade. Boosted by big data sets, new methods for inference and prediction are transforming many fields of science and technology. How will these developments affect the neurosciences? Bzdok & Yeo (pp2016) take a stab at this question in a wide-ranging review of recent analyses of brain data with modern methods.
Their review paper is organised around four key dichotomies among approaches to data analysis. I will start by describing these dichotomies from my own perspective, which is broadly – though not exactly – consistent with Bzdok & Yeo’s.
- Generative versus discriminative models: A generative model is a model of the process that generated the data (mapping from latent variables to data), whereas a discriminative model maps from the data to selected variables of interest.
- Nonparametric versus parametric models: Parametric models are specified using a finite number of parameters and thus their flexibility is limited and cannot grow with the amount of data available. Nonparametric models can grow in complexity with the data: The set of numbers identifying a nonparametric model (which may still be called “parameters”) can grow without a predefined limit.
- Bayesian versus frequentist inference: Bayesian inference starts by defining a prior over all models believed possible and then infers the posterior probability distribution over the models and their parameters on the basis of the data. Frequentist inference identifies variables of interest that can be computed from data and constructs confidence intervals and decision rules that are guaranteed to control the rate of errors across many hypothetical experimental analyses.
- Out-of-sample prediction and generalisation versus within-sample explanation of variance: Within-sample explanation of variance attempts to best explain a given data set (relying on assumptions to account for the noise in the data and control overfitting). Out-of-sample prediction integrates empirical testing of the generalisation of the model to new data (and optionally to different experimental conditions) into the analysis, thus testing the model, including all assumptions that define it, more rigorously.
Generative models are more ambitious than discriminative models in that they attempt to account for the process that generated the data. Discriminative models are often leaner – designed to map directly from data to variables of interest, without engaging all the complexities of the data-generating process.
Nonparametric models are more flexible than parametric models and can adapt their complexity to the amount of information contained in the data. Parametric models can be more stable when estimated with limited data and can sometimes support more sensitive inference when their strong assumptions hold.
Philosophically, Bayesian inference is more attractive than frequentist inference because it computes the probability of models (and model parameters) given the givens (or in Latin: the data). In real life, also, Bayesian inference is what I would aim to roughly approximate to make important decisions, combining my prior beliefs with current evidence. Full Bayesian inference on a comprehensive generative model is the most rigorous (and glamorous) way of making inferences. Explicate all your prior knowledge and uncertainties in the model, then infer the probability distribution over all states of the world deemed possible given what you’ve been given: the data. I am totally in favour of Bayesian analysis for scientific data analysis from the armchair in front of the fireplace. It is only when I actually have to analyse data, at the very last moment, that I revert to frequentist methods.
My only problem with Bayesian inference is my lack of skill. I never finish enumerating the possible processes that might have given rise to the data. When I force myself to stop enumerating, I don’t know how to implement the (incomplete) list of possible processes in models. And if I forced myself to make the painful compromises to implement some of these processes in models, I wouldn’t know how to do approximate inference on the incomplete list of badly implemented models. I would know that many of the decisions I made along the way were haphazard and inevitably subjective, that all them constrain and shape the posterior, and that few of them will be transparent to other researchers. At that point frequentist inference with discriminative models starts looking attractive. Just define easy-to-understand statistics of interest that can efficiently be computed from the data and estimate them with confidence intervals, controlling error probability without relying on subjective priors. Generative-model comparisons, as well, are often easier to implement in the frequentist framework.
Regarding the final dichotomy, out-of-sample prediction using fitted models provides a simple empirical test of generalisation. It can be used to test for generalisation to new measurements (e.g. responses to the same stimuli as in decoding) or to new conditions (as in cross-decoding and in encoding models, e.g. Kay et al. 2008; Naselaris et al. 2009). Out-of-sample prediction can be applied in crossvalidation, where the data are repeatedly split to maximise statistical efficiency (trading off computational efficiency).
Out-of-sample prediction tests are useful because they put assumptions to the test, erring on the safe side. Let’s say we want to test if two patterns are distinct and we believe the noise is multinormal and equal for both conditions. We could use a within-sample method like multivariate analysis of variance (MANOVA) to perform this test, relying on the assumption of multinormal noise. Alternatively, we could use out-of-sample prediction. Since we believe that the noise is multinormal, we might fit a Fisher linear discriminant, which is the Bayes-optimal classifier in this scenario. This enables us to project held-out data onto a single dimension, the discriminant, and use simpler inference statistics and fewer assumptions to perform the test. If multinormality were violated, the classifier would no longer be optimal, making prediction of the labels for held-out data work worse. We would more frequently err on the safe side of concluding that there is no difference, and the false-positives rate would still be controlled. MANOVA, by contrast, relies on multinormality for the validity of the test and violations might inflate the false-positives rate.
More generally, using separate training and test sets is a great way to integrate the cycle of exploration (hypothesis generation, fitting) and confirmation (testing) into the analysis of a single data set. The training set is used to select or fit, thus restricting the space of hypotheses to be tested. We can think of this as generating testable hypotheses. The training set helps us go from a vague hypothesis we don’t know how to test to a specifically defined hypothesis that is easy to test. The reason separate training and test sets are standard practice in machine learning and less widely used in statistics is that machine learning has more aggressively explored complex models that cannot be tested rigorously any other way. More on this here.
Out-of-sample prediction is not the alternative to p values
One thing I found uncompelling (though I’ve encountered it before, see Fig. 1) is the authors’ suggestion that out-of-sample prediction provides an alternative to null-hypothesis significance testing (NHST). Perhaps I’m missing something. In my view, as outlined above, out-of-sample prediction (the use of independent test sets) enables us to use one data set to restrict the hypothesis space (training) and another data set to do inference on the more specific hypotheses, which are easier to test with fewer assumptions. The prediction is the restricted hypothesis space. Just like within-sample analyses, out-of-sample prediction requires a framework for performing inference on the hypothesis space. This framework can be either frequentist (e.g. NHST) or Bayesian.
For example, after fitting encoding models to a training data set, we can measure the accuracy with which they predict the test set. The fitted models have all their parameters fixed, so are easy to test. However, we still need to assess whether the accuracy is greater than 0 for each model and whether one model has greater accuracy than another.
Using up one part of the data to restrict the hypothesis space (fitting) and then using another to perform inference on the restricted hypothesis space (so as to avoid the bias of training set accuracy that results from overfitting) could be viewed as a crude approximation (vacillating between overfitting on one set and using another to correct) to the rigorous thing to do: updating the current probability distribution over all possibilities as each data point is encountered.
Figure 1: I don’t understand why some people think of out-of-sample prediction as an alternative to p values.
Bzdok & Yeo do a good job of appreciating the strengths and weaknesses of either choice of each of these dichotomies and considering ways to combine the strengths even of apparently opposed choices. Four boxes help introduce the key dichotomies to the uninitiated neuroscientist.
The paper provides a useful tour through recent neuroscience research using advanced analysis methods, with a particular focus on neuroimaging. The authors make several reasonable suggestions about where things might be going, suggesting that future data analyses will…
- leverage big data sets and be more adaptive (using nonparametric models)
- incorporate biological structure
- combine the strengths of Bayesian and frequentist techniques
- integrate out-of-sample generalisation (e.g. implemented in crossvalidation)
Weaknesses of the paper in its current form
The main text moves over many example studies and adds remarks on analysis methodology that will not be entirely comprehensible to a broad audience, because they presuppose very specialised knowledge.
Too dense: The paper covers a lot of ground, making it dense in parts. Some of the points made are not sufficiently developed to be fully compelling. It would also be good to reflect on the audience. If the audience is supposed to be neuroscientists, then many of the technical concepts would require substantial unpacking. If the audience were mainly experts in machine learning, then the neuroscientific concepts would need to be more fully explained. This is not easy to get right. I will try to illustrate these concerns further below in the “particular comments” section.
Too uncritical: A positive tone is a good thing, but I feel that the paper is a little too uncritical of claims in the literature. Many of the results cited, while exciting for the sophisticated models that are being used, stand and fall with the model assumptions they are based on. Model checking and comparison of many alternative models are not standard practice yet. It would be good to carefully revise the language, so as not to make highly speculative results sound definitive.
No discussion of task-performing models: The paper doesn’t explain what from my perspective is the most important distinction among neuroscience models: Do they perform cognitive tasks? That this distinction is not discussed in detail reflects the fact that such models are still rare in neuroscience. We use a lot of different kinds of model, but even when they are generative and causal and constrained by biological knowledge, they are still just data-descriptive models in the sense that they do not perform any interesting brain information processing. Although they may be stepping stones toward computational theory, such models do not really explain brain computation at any level of abstraction. Task-performing computational models, as introduced by cognitive science, are first evaluated by their ability to perform an information-processing function. Recently, deep neural networks that can perform feats of intelligence such as object recognition have been used to explain brain and behavioural data (Yamins et al. 2013; 2014: Khaligh-Razavi et al. 2014; Cadieu et al. 2014; Guclu & van Gerven 2015). For all their abstractions, many of their architectural features are biologically plausible and at least they pass the most basic test for a computational model of brain function: explaining a computational function (for reviews, see Kriegeskorte 2015; Yamins & DiCarlo 2015).
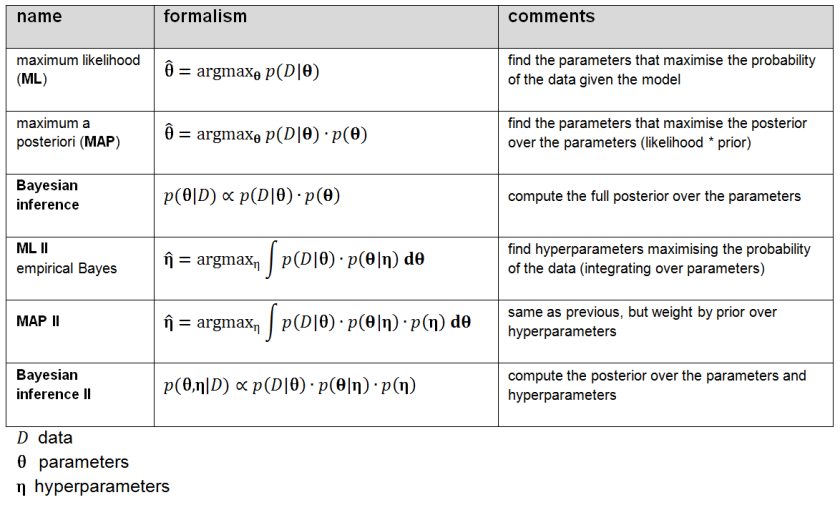Figure 2: Shades of Bayes. The authors follow Kevin Murphy’s textbook in defining degrees of Bayesianity of inference, ranging from maximum likelihood estimation (top) to full Bayesian inference on parameters and hyperparameters (bottom). Above is my slightly modified version.
Comments on specific statements
“Following many new opportunities to generate digitized brain data, uncertainties about neurobiological phenomena henceforth required assessment in the statistical arena.”
Noise in the measurements, not uncertainties about neurobiological phenomena, created the need for statistical inference.
“Finally, it is currently debated whether increasingly used “deep” neural network algorithms with many non-linear hidden layers are more accurately viewed as parametric or non-parametric.”
This is an interesting point. Perhaps the distinction between nonparametric and parametric becomes unhelpful when a model with a finite, fixed, but huge number of parameters is tempered by flexible regularisation. It would be good to add a reference on where this is “debated”.
“neuroscientists often conceptualize behavioral tasks as recruiting multiple neural processes supported by multiple brain regions. This century-old notion (Walton and Paul, 1901) was lacking a formal mathematical model. The conceptual premise was recently encoded with a generative model (Yeo et al., 2015). Applying the model to 10,449 experiments across 83 behavioral tasks revealed heterogeneity in the degree of functional specialization within association cortices to execute diverse tasks by flexible brain regions integration across specialized networks (Bertolero et al., 2015a; Yeo et al., 2015).”
This is an example of a passage that is too dense and lacks the information required for a functional understanding of what was achieved here. The model somehow captures recruitment of multiple regions, but how? “Heterogeneity in the degree of functional specialisation”, i.e. not every region is functionally specialised to exactly the same degree, sounds both plausible and vacuous. I’m not coming away with any insight here.
“Moreover, generative approaches to fitting biological data have successfully reverse engineered i) human facial variation related to gender and ethnicity based on genetic information alone (Claes et al., 2014)”
Fitting a model doesn’t amount to reverse engineering.
“Finally, discriminative models may be less potent to characterize the neural mechanisms of information processing up to the ultimate goal of recovering subjective mental experience from brain recordings (Brodersen et al., 2011; Bzdok et al., 2016; Lake et al., 2015; Yanga et al., 2014).”
Is the ultimate goal to “recover mental experience”? What does that even mean? Do any of the cited studies attempt this?
“Bayesian inference is an appealing framework by its intimate relationship to properties of firing in neuronal populations (Ma et al., 2006) and the learning human mind (Lake et al., 2015).”
Uncompelling. If the brain and mind did not rely on Bayesian inference, Bayesian inference would be no less attractive for analysing data from the brain and mind.
“Parametric linear regression cannot grow more complex than a stiff plane (or hyperplane when more input dimensions Xn) as decision boundary, which entails big regions with identical predictions Y.”
The concept of decision boundary does not make sense in a regression setting.
“Typical discriminative models include linear regression, support vector machines, decision-tree algorithms, and logistic regression, while generative models include hidden Markov models, modern neural network algorithms, dictionary learning methods, and many non-parametric statistical models (Teh and Jordan, 2010).”
Linear regression is not inherently either discriminative or generative, nor are neural networks. A linear regression model is generative when it predicts the data (either in a within-sample framework, such as classical univariate activation-based brain mapping, or in an out-of-sample predictive framework, such as encoding models). It is discriminative when it takes the data as input to predict other variables of interest (e.g. stimulus properties in decoding, or subject covariates).
“Box 4: Null-hypothesis testing and out-of-sample prediction”
As discussed above, this seems to me a false dichotomy. We can perform out-of-sample predictions and test them with null-hypothesis significance testing (NHST). Moreover, Bayesian inference (the counterpart to NHST) can operate on a single data set. It makes more sense to me to contrast out-of-sample prediction versus within-sample explanation of variance.
nikokriegeskorte 