Month: October 2017

[I7R5]

 

Wen, Shi, Chen, and Liu (pp2017) used a deep residual neural network (trained on visual object classification) as an encoding model to explain human cortical fMRI responses to movies. The deep net together with the encoding weights of the cortical voxels was then used to predict human cortical response patterns to 64K object images from 80 categories. This prediction serves, not to validate the model, but to investigate how cortical patterns (as predicted by the model) reflect the categorical hierarchy.

The authors report that the predicted category-average response patterns fall into three clusters corresponding to natural superordinate categories: biological things, nonbiological things, and scenes. They argue that these superordinate categories characterize the large-scale organization of human visual cortex.

For each of the three superordinate categories, the authors then thresholded the average predicted activity pattern and investigated the representational geometry within the supra-threshold volume. They find that biological things elicit patterns (within the subvolume responsive to biological things) that fall into four subclusters: humans, terrestrial animals, aquatic animals, and plants. Patterns in regions activated by scenes clustered into artificial and natural scenes. The patterns in regions activated by non-biological things did not reveal clear subdivisions.

The authors argue that this shows that superordinate categories are represented in global patterns across higher visual cortex, and finer-grained categorical distinctions are represented in finer-grained patterns within regions responding to superordinate categories.

This is an original, technically sophisticated, and inspiring paper. However, the title claim is not compellingly supported by the evidence. The fact that finer grained distinctions become apparent in pattern correlation matrices after restricting the volume to voxels responsive to a given category is not evidence for an association between brain-spatial scales and conceptual scales. To understand this, consider the fact that the authors’ analyses do not take the spatial positions of the voxels (and thus the spatial structure) into account at all. The voxel coordinates could be randomly permuted and the analyses would give the same results.

The original global representational dissimilarity (or similarity) matrices likely contain distinctions not only at the superordinate level, but also at finer-grained levels (as previously shown). When pattern correlation is used, these divisions might not be prominent in the matrices because the component shared among all exemplars within a superordinate category dominates. Recomputing the pattern correlation matrix after reducing the patterns to voxels responding strongly to a given superordinate category will render the subdivisions within the superordinate categories more prominent. This results from the mean removal implicit to the pattern correlation, which will decorrelate patterns that share high responses on many of the included voxels. Such a result does not indicate that the subdivisions were not present (e.g. significantly decodable from fMRI or even clustered) in the global patterns.

A simple way to take spatial structure into account would be to restrict the analysis to a single spatially contiguous cluster at a time, e.g. FFA. This is in fact the approach taken in a large number of previous studies that investigated the representations in category-selective regions (LOC, FFA, PPA, RSC, etc.). Another way would be to spatially filter the patterns and investigate whether finer semantic distinctions are associated with finer spatial scales. This approach has also been used in previous studies, but can be confounded by the presence of an unknown pattern of voxel gains (Freeman et al. 2013; Alink et al. 2017, Scientific Reports).

The approach of creating a deep net model that explains the data and then analyzing the model instead of the data is a very interesting idea, but also raises some questions. Clearly we need deep nets with millions of parameters to understand visual processing. If a deep net explains visual responses throughout the visual system and shares at least some architectural similarities with the visual hierarchy, then it is reasonable to assume that it might capture aspects of the computational mechanism of vision. In a sense, we have “uploaded” aspects of the mechanism of vision into the model, whose workings we can more efficiently study. This is always subject to consideration of alternative models whose architecture might better match what is known about the primate visual system and which might predict visual responses even better. Despite this caveat, I believe that developing deep net models that explain visual responses and studying their computational mechanisms is a promising approach in general.

In the present context, however, the goal is to relate conceptual levels of categories to spatial scales of cortical response patterns, which can be directly measured. Is the deep net really needed to address this? To study how categories map onto cortex, why not just directly study measured response patterns? This is fact is what the existing literature has done for years. The deep net functions as a fancy interpolator that imputes data where we have none (response patterns for 64K images). However, the 80 category-average response patterns could have been directly measured. Would this not be more compelling? It would not require us to believe that the deep net is an accurate model.

Although the authors have gotten off to a fresh start on the intriguing questions of the spatial organization of higher-level visual cortex, the present results do not yet go significantly beyond what is known and the novel and interesting methods introduced in the paper (perhaps the major contribution) raise a number of questions that should be addressed in a revision.

 

 

Strengths

• Presents several novel and original ideas for the use of deep neural net models to understand the visual cortex.
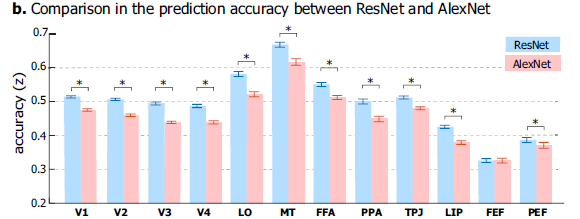
• Uses 50-layer ResNet model as encoding model and shows that this model performs better than the simpler AlexNet model.
• Tests deep net models trained on movie data for generalization to other movie data and prediction of responses in category-selective-region localizer experiments.
• Attempts to address the interesting hypothesis that larger scales of cortical organization serve to represent larger conceptual scales of categorical representation.
• The analyses are implemented at a high level of technical sophistication.

 

Weaknesses

• The central claim about spatial structure of cortical representations is not supported by evidence about the spatial structure. In fact, analyses are invariant to the spatial structure of the cortical response patterns.
• Unclear what added value is provided by the deep net for addressing the central claim that larger spatial scales in the brain are associated with larger conceptual scales.
• Uses a definition of “modularity” from network theory to analyze response pattern similarity structure, which will confuse cognitive scientists and cognitive neuroscientists to whom modularity is a computational and brain-spatial notion. Fails to resolve the ambiguities and confusions pervading the previous literature (“nested hierarchy”, “module”).
• Follows the practice in cognitive neuroscience of averaging response patterns elicited by exemplars of each category, although the deep net predicts response patterns for individual images. This creates ambiguity in the interpretation of the results.
• The central concepts modularity and semantic similarity are not properly defined, either conceptually or in terms of the mathematical formulae used to measure them.
• The BOLD fMRI measurements are low in resolution with isotropic voxels of 3.5 mm width.

 

Suggestions for improvements

 

(1) Analyze to what extent different spatial scales in cortex reflect information about different levels of categorization (or change the focus of the paper)

The ResNet encoding model is interesting from a number of perspectives, so the focus of the paper does not have to be on the association of spatial cortical and conceptual scales. If the paper is to make claims about this difficult, but important question, then analyses should explicitly target the spatial structure of cortical activity patterns.

The current analyses are invariant to where responses are located in cortex and thus fundamentally cannot address to what extent different categorical levels are represented at different spatial scales. While the ROIs (Figure 8a) show prominent spatial clustering, this doesn’t go beyond previous studies and doesn’t amount to showing a quantitative relationship.

The emergence of subdivisions within the regions driven by superordinate-category images could be entirely due to the normalization (mean removal) implicit to the pattern correlation. Similar subdivisions could exist in the complementary set of voxels unresponsive to the superordinate category, and/or in the global patterns.

Note that spatial filtering analyses might be interesting, but are also confounded by gain-field patterns across voxels. Previous studies have struggled to address this issue; see Alink et al. (2017, Scientific Reports) for a way to detect fine-grained pattern information not caused by a fine-grained voxel gain field.

 

(2) Analyze measured response patterns during movie or static-image presentation directly, or better motivate the use of the deep net for this purpose

The question how spatial scales in cortex relate to conceptual scales of categories could be addressed directly by measuring activity patterns elicited by different images (or categories) with fMRI. It would be possible, for instance, to measure average response patterns to the 80 categories. In fact previous studies have explored comparably large sets of images and categories.

Movie fMRI data could also be used to address the question of the spatial structure of visual response patterns (and how it relates to semantics), without the indirection of first training a deep net encoding model. For example, the frames of the movies could be labeled (by a human or a deep net) and measured response patterns could directly be analyzed in terms of their spatial structure.

This approach would circumvent the need to train a deep net model and would not require us to trust that the deep net correctly predicts response patterns to novel images. The authors do show that the deep net can predict patterns for novel images. However, these predictions are not perfect and they combine prior assumptions with measurements of response patterns. Why not drop the assumptions and base hypothesis tests directly on measured response patterns?

In case I am missing something and there is a compelling case for the approach of going through the deep net to address this question, please explain.

 

(3) Use clearer terminology

Module: The term module refers to a functional unit in cognitive science (Fodor) and to a spatially contiguous cortical region that corresponds to a functional unit in cognitive neuroscience (Kanwisher). In the present paper, the term is used in the sense of network theory. However it is applied not to a set of cortical sites on the basis of their spatial proximity or connectivity (which would be more consistent with the meaning of module in cognitive neuroscience), but to a set of response patterns on the basis of their similarity. A better term for this is clustering of response patterns in the multivariate response space.

Nested hierarchy: I suspect that by “nested” the authors mean that there are representations within the subregions responding to each of the superordinate categories and that by “hierarchy” they refer to the levels of spatial inclusion. However, the categorical hierarchy also corresponds to clusters and subclusters in response-pattern space, which could similarly be considered a “nested hierarchy”. Finally, the visual system is often characterized as a hierarchy (referring to the sequence of stages of ventral-stream processing). The paper is not sufficiently clear about these distinctions. In addition, terms like “nested hierarchy” have a seductive plausibility that belies their lack of clear definition and the lack of empirical evidence in favor of any particular definition. Either clearly define what does and does not constitute a “nested hierarchy” and provide compelling evidence in favor of it, or drop the concept.

 

(4) Define indices measuring “modularity” (i.e. response-pattern clustering) and semantic similarity

You cite papers on the Q index of modularity and the LCH semantic similarity index. These indices are central to the interpretation of the results, so the reader should not have to consult the literature to determine how they are mathematically defined.

 

(5) Clarify results on semantic similarity

The correlation between LCH semantic similarity and cortical pattern correlation is amazing (r=0.93). Of course this has a lot to do with the fact that LCH takes a few discrete values and cortical similarity was first averaged within each LCH value.

What is the correlation between cortical pattern similarity and semantic similarity…

• for each of the layers of ResNet before remixing to predict human fMRI responses?
• after remixing to predict human fMRI responses for each of a number of ROIs (V1-3, LOC, FFA, PPA)?
• for other, e.g. word-co-occurrence-based, semantic similarity measures (e.g. word2vec, latent semantic analysis)?

 

(6) Clarify the methods details

I didn’t understand all the methods details.

• How were the layer-wise visual feature sets defined? Was each layer refitted as an encoding model? Or were the weights from the overall encoding model used, but other layers omitted?
• I understand that the sub-divisions of the three superordinate categories were defined by k-means clustering and that the Q index (which is not defined in the paper) was used. How was the number k of clusters determined? Was k chosen to maximize the Q index?
• How were the category-associated cortical regions defined, i.e. how was the threshold chosen?

 

 

(7) Cite additional previous studies

Consider discussing the work of Lorraine Tyler’s lab on semantic representations and Thomas Carlson’s paper on semantic models for explaining similarity structure in visual cortex (Carlson et al. 2013, Journal of Cognitive Neuroscience).

[I5R6]

 

Majaj & Pelli (pp2017) give a brief overview of classification models in vision science, leading from linear discriminants and the perceptron to deep neural networks. They discuss some of the perks and perils of using machine learning, and deep learning in particular, in the study of biological vision.

This is a brief and light-footed review that will be of interest to vision scientists wondering whether and why to engage machine learning and deep learning in their own work. I enjoyed some of the thoughtful notes on the history of classification models and the sketch of the progression toward modern deep learning.

The present draft lists some common arguments for and against deep learning models, but falls short of presenting a coherent perspective on why deep learning is important for vision science, or not; or which aspects are substantial and which are hype. It also doesn’t really explain deep learning or how it relates to the computational challenge of vision.

The overall conclusion is that machine learning and deep learning are useful modern tools for the vision scientist. In particular, the authors argue that deep neural networks provide a “benchmark” to compare human performance to, replacing the optimal linear filter and signal detection theory as the normative benchmark for vision. This misses what I would argue is the bigger point: deep neural networks provide an entry point for modeling brain information processing and engaging the real problem of vision, rather than a toy version of the problem that lacks all of vision’s essential challenges.

 

Suggestions for improvements

(1) Clearly distinguish deep learning within machine learning

The abstract doesn’t mention deep learning at all. As I was reading the introduction, I was wondering if deep learning had been added to the title of a paper about machine learning in vision science at the very end. Deep learning is defined as “the latest version of machine learning”. This is incorrect. Rather than a software product that is updated in a sequence of versions, machine learning is a field that explores a wide variety of models and inference algorithms in parallel. The fact that deep learning (which refers to learning of deep neural network models) is getting a lot of attention at the moment does not mean that other approaches, notably Bayesian nonparametric models, have lost appeal. How is deep learning different? Does it matter more for vision than other approaches? If so, why?

 

(2) Explain why depth matters

The multiple stages of nonlinear transformation that define deep learning models are essential for many real-world applications, including vision. I think this point should be central as it explains why vision science needs deep models.

 

(3) Clearly distinguish the use of machine learning models to (a) analyze data and to (b) model brain information processing

The current draft largely fails to distinguish two ways of using machine learning in vision science: to analyze data (e.g. decode neuronal population codes) and to model brain information processing. Both are important, but the latter more fundamentally advances the field.

 

(4) Relate classification to machine learning more broadly and to vision

The present draft presents a brief history of classification models. Classification is a small (though perhaps arguably key?) problem within both machine learning and vision. Why is this particular problem the focus of such a large literature and of this review? How does it relate to other problems in machine learning and in vision?

 

(5) Separate the substance from the hype and present a coherent perspective

Arguments for and against deep learning are listed without evaluation or a coherent perspective. For example, is it true that deep learning models have “too many parameters”? Should we strive to model vision with a handful of parameters? Or do models need to be complex because vision requires complex domain knowledge? Do tests of generalization performance address the issue of overfitting? (No, no, yes, yes.) Note that the modern version of the statistical modeling, which is touted as more rigorous, is Bayesian nonparametrics – defined by no limits on the parametric complexity of a model.

 

(6) Consider addressing my particular comments below.

 

Particular comments

“Many perception scientists try to understand recognition by living organisms. To them, machine learning offers a reference of attainable performance based on learned stimuli.”

It’s not really a normative reference. There is an infinity of neural network models and performance of a particular one can never be claimed to be “ideal”. Deep learning is worse in this respect than the optimal linear filter (which provides a normative reference for a task – with the caveat that the task is not vision).

 

“Deep learning is the latest version of machine learning, distinguished by having more than three layers.”

It’s not the “latest version”, rather it’s an old variant of machine learning that is currently very successful and popular. Also, a better definition of deep is that there is more than one hidden layer intervening between input and output layers.

 

“It is ubiquitous in the internet.”

How is this relevant?

 

“Machine learning shifts the emphasis from how the cells encode to what they encode, i.e. from how they encode the stimulus to what that code tells us about the stimulus. Mapping a receptive field is the foundation of neuroscience (beginning with Weber’s 1834/1996 mapping of tactile “sensory circles”), but many young scientists are impatient with the limitations of single-cell recording: looking for minutes or hours at how one cell responds to each of perhaps a hundred different stimuli. New neuroscientists are the first generation for whom it is patently clear that characterization of a single neuron’s receptive field, which was invaluable in the retina and V1, fails to characterize how higher visual areas encode the stimulus. Statistical learning techniques reveal “how neuronal responses can best be used (combined) to inform perceptual decision-making” (Graf, Kohn, Jazayeri, & Movshon, 2010).”

This is an important passage. It’s true that single neurons in inferior temporal cortex, for example, might be (a) difficult to characterize singly with tuning functions, (b) idiosyncratic to a particular animal, and (c) so many in number and variety that characterizing them one by one seems hopeless. It therefore appears more productive to focus on understanding the population code. However, it is not only what is encoded in the population, but also how it is encoded. The format determines what inferences are easy given the code. For example, we can ask what information could be gleaned by a single downstream neuron computing a linear or radial-basis-function readout of the code.

 

“For psychophysics, Signal Detection Theory (SDT) proved that the optimal classifier for a signal in noise is a template matcher (Peterson, Birdsall, & Fox, 1954; Tanner & Birdsall, 1958).”

Detecting chihuahuas in complex scenes can be considered an example of detecting “signal in noise”, and it is an example of a visual task. A template matcher is certainly not optimal for this problem (in fact it will fail severely at this problem). It would help here to define signal and noise.

The problem of detecting a fixed pattern in Gaussian noise needs to be explained first in any course of vision, so as to inoculate students against the misconstrual of the problem of vision it represents. On a more conciliatory note, one could argue that although detecting a fixed pattern in noise is a misleading oversimplification of vision, it captures a component of the problem. The optimal solution to this problem, template matching, captures a component of the solution to vision. Deep feedforward neural networks could be described as hierarchical template matchers, and they do seem to capture some aspects of vision.

 

“SDT has been a very useful reference in interpreting human psychophysical performance (e.g. Geisler, 1989; Pelli et al., 2006). However, it provides no account of learning. Machine learning shows promise of guiding today’s investigations of human learning and may reveal the constraints imposed by the training set on learning.”

In addition to offering learning algorithms that might relate to how brains learn, machine learning enables us to use realistically complex models at all.

 

“It can be hard to tell whether behavioral performance is limited by the set of stimuli, or the neural representation, or the mismatch between the neural decision process and the stimulus and task. Implications for classification performance are not readily apparent from direct inspection of families of stimuli and their neural responses.”

Intriguing, but cryptic. Please clarify.

 

“Some biologists complain that neural nets do not match what we know about neurons (Crick, 1989; Rubinov, 2015).”

It is unclear how the ideal “match” should even be defined. All models abstract, and that is their purpose. Stating a feature of biology that is absent in the model does not amount to a valid criticism. But there is a more detailed case to be made for incorporating more biologically realistic dynamic components, so please elaborate.

 

“In particular, it is not clear, given what we know about neurons and neural plasticity, whether a backpropagation network can be implemented using biologically plausible circuits (but see Mazzoni et al., 1991, and Bengio et al., 2015).”

Neural net models can be good models of perception without being good models of learning. There has also been a recent resurgence in work exploring how backpropagation, or a closely related form of credit assignment, might be implemented in brains. Please discuss the work along these lines by Senn, Richards, Bogacz, and Bengio.

 

“Some biological modelers complain that neural nets have alarmingly many parameters. Deep neural networks continue to be opaque”

Why are many parameters “alarming” from the more traditional perspective on modeling? Do you feel that the alarm is justified? My view is that the history of AI has shown that intelligence requires rich domain knowledge. Simple models therefore will not be able to explain brain information processing. Machine learning has taught us how to learn complex models and avoid their pitfalls (overfitting).

 

“Some statisticians worry that rigorous statistical tools are being displaced by machine learning, which lacks rigor (Friedman, 1998; Matloff, 2014, but see Breiman, 2001; Efron & Hastie, 2016).”

The classical simple models can’t cut it, so their rigour doesn’t help us. Machine learning has boldly engaged complex models as are required for AI and brain science. To be able to do this, it initially took a pragmatic computational, rather than a formal probabilistic approach. However, machine learning and statistics have since grown together in many ways, providing a very general perspective on probabilistic inference that combines complexity and rigor.

 

“It didn’” (p. 9) Fragment.

 

“Unproven convexity. A problem is convex if there are no local minima other than the global minimum.”

I think this is not true. Here’s my current understanding: If a problem is convex, then any local minimum is the global minimum. This is convenient for optimization and provably not the case for neural networks. However, the reverse implication does not hold: if every local minimum is a global minimum, the function is not necessarily convex. There is a category of cost functions that are not convex, but every local minimum is a global minimum. Neural networks appear to fall in this category (at least under certain conditions that tend to hold in practice).

Note that there can be multiple global minima. In fact, the error function of a neural network over the weight domain typically has many symmetries, with any given set of weights having many computationally equivalent twins (i.e. the model computes the same overall function for different parameter settings). The high dimensionality, however, is not a curse, but a blessing for gradient descent: In a very high-dimensional weight space, it is unlikely that we find ourselves trapped, with the error surface rising in all directions. There are too many directions to escape in. Several papers have argued that local minima are not an issue for deep learning. In particular, it has been argued that every local minimum is a global minimum and that every other critical point is a saddle point, and that saddle points are the real challenge. Moreover, deep nets with sufficient parameters can fit the training data perfectly (interpolating), while generalizing well (which, surprisingly, some people find surprising). There is also evidence that stochastic gradient descent finds flat minima corresponding to robust solutions.

“This [convexity] guarantees that gradient-descent will converge to the global minimum. As far as we know, classifiers that give inconsistent results are not useful.”

That doesn’t follow. A complex learner, such as an animal or neural net model, with idiosyncratic and stochastic initialization and experience may converge to an idiosyncratic solution that is still “useful” – for example, classifying with high accuracy and a small proportion of idiosyncratic errors.

 

“Conservation of a solution across seeds and algorithms is evidence for convexity.”

No, but it may be evidence for a minimum with a large basin of attraction. Would need to define what counts as conservation of a solution: (1) identical weights, (2) computationally equivalent weights (same input-output mapping). Definition 2 seems more helpful and relevant.

 

““Adversarial” examples have been presented as a major flaw in deep neural networks. These slightly doctored images of objects are misclassified by a trained network, even though the doctoring has little effect on human observers. The same doctored images are similarly misclassified by several different networks trained with the same stimuli (Szegedy, et al., 2013). Humans too have adversarial examples. Illusions are robust classification errors. […] The existence of adversarial examples is intrinsic to classifiers trained with finite data, whether biological or not.”

I agree. We will know whether humans, too, are susceptible to the type of adversarial example described in the cited paper, as soon as we manage to backpropagate through the human visual system so as to construct comparable adversarial examples for humans.

 

“SDT solved detection and classification mathematically, as maximum likelihood. It was the classification math of the sixties. Machine learning is the classification math of today. Both enable deeper insight into how biological systems classify. In the old days we used to compare human and ideal classification performance. Today, we can also compare human and machine learning.”

“…the performance of current machine learning algorithms is a useful benchmark”

SDT is classification math for linear models, ML is classification math for more complex models. These models enable us to tackle the real problem of vision. Rather than comparing human performance to a normative ideal of performance on a toy task, we can use deep neural networks to model the brain information processing underlying visual recognition. We can evaluate the models by comparing their internal representations to brain representations and their behavior to human behavior, including not only the ways they shine, but also the ways they stumble and fail.

 

 

[I8R8]

 

Yang, Song, Newsome, and Wang (pp2017) trained a rate-coded recurrent neural network with 256 hidden units to perform a variety of classical cognitive tasks. The tasks combine a number of component processes including evidence accumulation over time, multisensory integration, working memory, categorization, decision making, and flexible mapping from stimuli to responses. The tasks include:

• speeded response indicating the direction of the stimulus (stimulus-response mapping)
• speeded response indicating the opposite of the direction of the stimulus (flexible stimulus-response mapping)
• response indicating the direction of a stimulus after a delay during which the stimulus is not visible (working memory)
• decision indicating which of two noisy stimulus inputs is stronger (evidence accumulation)
• decision indicating which of two ranges of the stimulus variable the stimulus falls in (categorization)

The 20 distinct tasks result from combining in various ways the requirements of accumulating stimulus evidence from two sensory modalities, maintaining stimulus evidence in working memory during a delay, deciding which category the stimulus fell in, and flexible mapping to responses.

The tasks reduce cognition to its bare bones and the model abstracts from the real-world challenges of perception (pattern recognition) and motor control, so as to focus on the flexible linkage between perception and action that we call cognition. The input to the model includes a “fixation” signal, sensory stimuli varying along a single circular dimension, and an rule input, that specifies a task index.

The fixation signal is given through a special unit, whose activity corresponds to the presence of a fixation dot on the screen in front of a primate subject. The fixation signal accompanies the perceptual and maintenance phases of the task, and its disappearance indicates that the primate or model should respond. The sensory stimulus (“direction of stimulus from fixation”) is encoded in a set of direction-tuned units representing the circular dimension. Each of two sensory modalities is represented by such a set of units. The task rule is entered in one-hot format through a set of task units that receive the task index throughout performance of a task (no need to store the current task in working memory). The motor output is a “saccade direction” encoded, similarly to the stimulus, by a set of direction-tuned units.

Such tasks have long been used in nonhuman primate cell recording and human imaging studies, and also in rodent studies, in order to investigate how basic building blocks of cognition are implemented in the brain. This paper provides an important missing link between primate cognitive neurophysiology and rate-coded neural networks, which are known to scale to real-world artificial intelligence challenges.

Unsurprisingly, the authors find that the network learns to perform all 20 tasks after interleaved training on all of them. They then perform a number of well-motivated analyses to dissect the trained network and understand how it implements its cognitive feats.

An important question is whether particular units serve task-specific or task-general functions. One extreme hypothesis is that each task is implemented in a separate set of units. The opposite hypothesis is that all tasks employ all units. In order to address the degree of task-generality of the units, the authors measure the extent to which each unit conveys relevant information in each task. This is measured by the variance of a unit’s activity across different  conditions within a task (termed the task variance). The authors find that the network learns to share some of the dynamic machinery it learns among different tasks.

The authors find evidence for a compositional implementation of the tasks in the trained network. Compositionality here means that the tasks employ overlapping sets of functional components of the network. Rather than learning a separate dynamic systems for each task, the network appears to learn dynamic components serving different functions that can be flexibly combined to enable performance of a wide range of tasks.

The authors’ argument in favor of a compositional architecture is based on two observations: (1) Pairs of tasks that share cognitive component functions tend to involve overlapping sets of units. (2) Task-rule inputs, though trained in one-hot format, can be linearly combined (e.g. Delay Anti = Anti + Delay Go – Go) and the network given such a task specification (which it has never been trained on) will perform the implied task with high accuracy.

 

These analyses are interesting because they help us understand how the network works and because they can also be applied to primate cell recordings and help us compare models to brains.

When the network is sequentially trained on one task at a time, the learning of new tasks interferes with previously acquired tasks, reducing performance. However, a continual learning technique that selectively protects certain learned connections enabled sequential acquisition of multiple tasks.

Overall, this is a highly original paper presenting a simple, yet well-motivated model and several useful analysis methods for understanding biological and artificial neural networks. The model extends the authors’ previous work on the neural implementation of some of these components of cognition. Importantly, the paper helps strengthen the link between rate-coded neural network models and primate (and rodent) cognitive neuroscience.

 

Strengths

• The model is simple and well-designed and helps us imagine how basic components of cognition might be implemented in a recurrent neural network. It is essential that we build task-performing models to complement our fallible intuitions as to the signatures of cognitive processes we should expect in neuronal recordings.
• The paper links primate cognitive neurophysiology to rate-coded neural networks trained with stochastic gradient descent. This might help boost future interactions between neurophysiologists and engineers.
• The measures and analyses introduced to dissect the network are well-motivated, straightforward, and imaginative. Several of them can be equally applied to models and neuronal recordings.
• The paper is well-written, clear, and tells an interesting story.
• The figures are of high quality.

 

Weaknesses

• The tasks are so simple that they do not pose substantial computational challenges. This is a strength because it makes it easier to understand neuronal responses in primate brains and unit responses in models. We have to start from the simplest instances of cognition. However, it is also a weakness. Consider the comparison to understanding the visual system. One approach is to reduce vision to discriminating two predefined images. The optimal algorithm for this task is a linear filter applied to the image. The intuitive reduction of vision to this scenario supports the template-matching model. However, this task and its optimal solution fundamentally misconstrues the challenge of visual recognition in the real world, which has to deal with complex accidental variation within each category to be recognized. The dominant current vision model is provided by deep neural networks, which perform multiple stages of nonlinear transformation and learn rich knowledge about the world. Simple cognitive tasks provide a starting point, but – like the two-image discrimination task in vision – abstract away many essential features of cognition. In vision, models are tested in terms of their performance on never seen images – a generalization challenge at the heart of what vision is all about. In cognition as well, we ultimately have to engage complex tasks and test models in terms of their ability to generalize to new instances drawn randomly from a very complex space. The paper leaves me wondering how we can best take small steps from the simple tasks dominating the literature toward real-world cognitive challenges.
• The paper does not compare a variety of models. Can we learn about the mechanism the brain employs without comparing alternative models? Rate-coded recurrent neural networks are universal approximators of dynamical systems. This property is independent of particular choices defining the units. It is entirely unsurprising that such a model, trained with stochastic gradient descent, can learn these tasks (and the supertask of performing all 20 of them). Given the simplicity of the tasks, it is also not surprising that 256 recurrent units suffice. In fact, the authors report that the results are robust between 128 and 512 recurrent units. The value of this project consists in the way it extends our imagination and generates hypotheses (to be tested with neuronal recordings) about the distributions of task-specific and task-general units. The simplicity of the model and its gradient descent training provides a compelling starting point. However, there are infinite ways a recurrent neural network might implement performance at these tasks. It will be important to contrast alternative task-performing models and adjudicate between them with brain and behavioral data.
• The paper does not include analyses of biological recordings or behavioral data, which could help us understand the degree to which the model resembles or differs from the primate brain in the way it implements task performance.

Addressing all of these weaknesses could be considered beyond the scope of the current paper. But the authors should consider if they can go toward addressing some of them.

 

Suggested improvements

(1) It might be useful to explicitly model the 20 tasks in terms of cognitive component functions (multisensory integration, evidence accumulation, working memory, inversion of stimulus-response mapping, etc.). The resulting matrix could be added to Table 1 or shown separately. This compositional cognitive description of the tasks could be used to explain the patterns of unit involvement in different tasks (e.g. as measured by task variance) using a linear model. The compositional model could then be inferentially compared to a non-compositional model in which each task is has a single cognitive component function. This more hypothesis-driven approach might help to address the question of compositionality inferentially.

(2) The depiction of the neural network model in Figure 1 could give a better sense of the network complexity and architecture. Instead of the three-unit icon in the middle, how about a directed graph with 256 dots, one for each recurrent unit, and a separate circular arrangements of input and output units (how many were there?). Instead of the network-unit icon with the cartoon of the nonlinear activation, why not show the actual softplus function?

(3) It would the good to see the full 256² connectivity matrix (ordered by clusters) and the network as a graph with nodes arranged by proximity in the connectivity matrix and edges colored to indicate the weights.

(4) The paper states that “the network can maintain information throughout a delay period of up to five seconds.” What does time in seconds mean in the context of the model? Is time meaningful because the units have time constants similar to biological neurons? It would be good to add supplementary text and perhaps a figure that explains how the pace of processing is matched to biological neural networks. If the pace is not compellingly matched, on the other hand, then perhaps real time units (e.g. seconds) should not be used when describing the model results.

(5) Please clarify whether the hidden units are fully recurrently connected. It would also be good to extend the paper to report how the density of recurrent connectivity affects task performance, learning, clustering and compositionality.

(6) The initial description of task variance is not entirely clear. State explicitly that one task variance estimate is computed for each task, reflecting the response variance across conditions within that task, and thus providing a measure of the stimulus-information conveyed during the task.

(7) Clustering is useful here as an exploratory and descriptive technique for dissecting the network, carving the model at its joints. However, clustering methods like k-means always output clusters, even when the data are drawn from a unimodal continuous distribution. The title claim of “clusters” thus should ideally be substantiated (by  inferential comparison to a continuous model) or dropped.

(8) The clustering will depend on the multivariate signature used to characterize each unit. Instead of task variance patterns, a unit’s connectivity (incoming and outgoing) could be used as a signature and basis of clustering. How do results compare for this method? My guess is that using the task variance pattern across tasks tends to place units in the same cluster if they contribute to the same task, although they might represent different stimulus information in the task. If this is the motivation, it would be good to explain it more explicitly.

(9) It is an interesting question whether units in the same cluster serve the same function. (It seems unlikely in the present analyses, but would be more plausible if clustering were based on incoming and outgoing weights.) The hypothesis that units in a cluster serve the same function could be made precise by saying that the units in a cluster share the same patterns of incoming and outgoing connections, except for weight noise resulting from the experiential and internal noise during training. Under this hypothesis incoming weights are exchangeable among units within the same cluster. The same holds for outgoing weights. The hypothesis could, thus, be tested by shuffling the incoming and the outgoing weights within each cluster and observing performance. I would expect performance to drop after shuffling and would interpret this as a reminder that the cluster-level summary is problematic. Alternatively, to the extent that clusters do summarize the network well, one might try to compress the network down to one unit per cluster, by combining incoming and outgoing weights (with appropriate scaling), or by training a cluster-level network to approximate the dynamics of the original network.

(10) The method of t-SNE is powerful, but its results strongly depend on the parameter settings, creating an issue of researcher degrees of freedom. Moreover, the objective function is difficult to state precisely in a single sentence (if you disagree, please try). Multidimensional scaling by contrast uses a range of objective functions that are easy to define in a single sentence. I wonder why t-SNE should be preferred in this particular context.

(11) Another way to address compositionality would be to assess whether a new task can be more rapidly acquired if its components have been trained as part of other tasks previously.

(12) In Fig. 3 c and e, label the horizontal axis (cluster).

(13) It is great that the Tensorflow implementation will be shared. It would be good if the model data could also be shared in formats useful to people using Python as well as Matlab. This could be a great resource for students and researchers. Please state more completely in the main paper exactly what (Python code? Task and model code? Model data?) will be available where (Github?).

(14) After sequential training, performance at multisensory delayed decision making does not appear to suffer compared to interleaved training. Was this because multisensory delayed decision making was always the last task (thus not overwritten) or is it more robust because it shares more components with other tasks?

(15) A better word for “linear summation” is “sum”.