Our retinae sample the images in our eyes discretely, conveying a million local measurements through the optic nerve to our brains. Given this piecemeal mess of signals, our brains infer the structure of the scene, giving us an almost instant sense of the geometry of the environment and of the objects and their relationships.
We see the world in terms of objects. But how our visual system defines what an object is and how it represents objects is not well understood. Two key properties thought to define what an object is in philosophy and psychology are spatiotemporal continuity and cohesion (Scholl 2007). An object can be thought of as a constellation of connected parts, such that if we were to pull on one part, the other parts would follow along, while other objects might stay put. Because the parts cohere, the region of spacetime that corresponds to an object is continuous. The decomposition of the scene into potentially movable objects is a key abstraction that enables us to perceive, not just the structure and motion of our surroundings, but also the proclivities of the objects (what might drop, collapse, or collide) and their affordances (what might be pushed, moved, taken, used as a tool, or eaten).
An important computational problem our visual system must solve, therefore, is to infer what pieces of a retinal image belong to a single object. This problem has been amply studied in humans and nonhuman primates using behavioral experiments and measurements of neural activity. A particular simplified task that has enabled highly controlled experiments is mental line tracing. A human subject or macaque fixating on a central cross is presented with a display of multiple curvy lines, one of which begins at the fixation point. The task is to judge whether a peripheral red dot is on that line or on another line (called a distractor). Behavioral experiments show that the task is easy to the extent that the target line is short or isolated from any distractors. Adding distractor lines in the vicinity of the target line to clutter up the scene and making the target line long and curvy makes the task more difficult. If the target snakes its way through complex clutter closeby, it is no longer instantly obvious where it leads and attention and time are required to judge whether the red dot is on the target or on a distractor line.
Our reaction time is longer when the red dot is farther from fixation along the target line. This suggests that the cognitive process required to make the judgment involves tracing the line with a sequential algorithm, even when fixation is maintained at the central cross. However, the reaction time is not in general linear in the distance, measured along the line, between the fixation point and the dot, as would be predicted by sequential tracing of the line at constant speed. Instead, the speed of tracing is variable depending on the presence of distracting lines in the vicinity of the current location of the tracing process along the target line. Tracing proceeds more slowly when there are distracting lines close by and more quickly when the distracting lines are far away.
The hypothesis that the primate visual system traces the line sequentially from the fixation point is supported by seminal electrophysiological experiments by Pieter Roelfsema and colleagues, which have shown that neurons in early visual cortex that represent particular pieces of the line emanating from the fixation point are upregulated in sequence, consistent with a sequential tracing process. This sequential upregulation of activity of neurons representing progressively more distal portions of the line is often interpreted as the neural correlate of attention spreading from fixation along the attended line during task performance.
The variation in speed of the tracing process can be explained by the attentional growth-cone hypothesis (Pooresmaeili & Roelfsema 2014) which posits that attention spreads not only in the primary visual cortex but also at higher levels of cortical representation. This hypothesis can explain the variation in tracing speed: At higher levels of cortical visual representation, neurons have larger receptive fields and offer a coarser-scale summary of the image, enabling the tracing to proceed at greater speed along the line in the image. In the absence of distractors, tracing can proceed quickly at a high-level of representation. However, in the presence of distractors, the higher-level representations may not be able to resolve the scene at a sufficient grain, and tracing must proceed more slowly in lower-level representations.
Higher-level neurons are more likely to suffer from interference from distractor lines within their larger receptive fields. If a distractor line is present in a neuron’s receptive field, the neuron may not respond as strongly to the line being traced, effectively blocking the path for sequential tracing in the high-level representation. However, tracing can continue – more slowly – at lower levels, where receptive fields are small enough to discern the line without interference.
Now Schmid & Neumann (pp2024) offer a brain-computational model explaining in detail how this multiscale algorithm for attentional selection of the line emanating from the fixation point might be implemented in the primate brain. They describe a mechanistic model and demonstrate by simulation that it can explain how mental line tracing might be implemented in the primate brain.
Pyramidal neurons at multiple levels of the visual hierarchy (corresponding to cortical areas V1, V2, V4) detect local oriented line segments on the basis of the bottom-up signals arriving at their basal dendritic integration sites. These line segments are pieces of the target and distractor lines, represented in each area at a different scale of representation. The pyramidal neurons also receive lateral and top-down input providing contextual information at their apical dendritic integration sites, enabling them to sense whether the line segment they are representing is part of a longer continuous line.
The attentional “label” indicating that a neuron represents a piece of the target line is encoded by an upregulation of the activity of the pyramidal neurons, consistent with neural recording results from Roelfsema and colleagues (1998). The upregulation of activity, i.e. the attention label, can spread laterally within a single area such as V1. Connectivity between neurons representing approximately collinear line segments implements an inductive bias that favors interpretations conforming to the Gestalt principle of good continuation. However, the upregulation will spread only to pyramidal neurons that (1) are activated by the stimulus, (2) receive contextual input from pyramidal neurons representing approximately collinear line segments, and (3) receive thalamic input indicating the local presence of the attentional marker.
Each step of propagation is conditioned on the conjunction of these three criteria. The neural computations could be implemented exploiting the intracellular dynamics in layer-5 pyramidal neurons, where dendritic inputs entering at apical integration sites cannot drive a response by themselves but can modulate responses to inputs entering at basal integration sites. An influential theory suggests that contextual inputs arriving at the apical dendritic integration sites modulate the response to bottom-up stimulus inputs arriving at the basal dendritic integration sites (Larkum 2013, BrainInspired podcast). Schmid and Neumann’s model further posits that the apical inputs are gated by thalamic inputs (Halassa & Kastner 2017), implementing a test of the third criterion for propagation of the attentional label.
The attentional label is propagated locally from already labeled pyramidal neurons to pyramidal neurons at all levels of the visual hierarchy that represent closeby line segments sufficiently aligned in orientation to be consistent with their being part of the target line. To enable the coarser-scale representations in higher cortical areas to speed the process, neurons representing the same patch of the visual field at different scales are connected through thalamocortical loops. Through the thalamus, each level is connected to all other levels, enabling label propagation to bypass the stages of the hierarchy. The thalamic component (possibly in the pulvinar region of the visual thalamus) represents a map of the labeled locations, but not detailed orientation information.
Imagine a mechanical analogy, in which tube elements represent local segments of the lines. The stimulus-driven bottom-up signals align the orientations of the tube elements with the orientations of the line segments they represent, so the tube elements turn to form long continuous tunnels depicting the lines. A viscous liquid is injected into the tube element representing the fixation point and spreads. Adjacent tube elements need to be aligned for the liquid to flow from one into the other. In addition, there are valves between the tube elements, which open only in the presence of thalamic input. Importantly, the viscous liquid can flow not only at the V1 level of representation, where the tube elements represent tiny pieces of the lines and the viscous liquid needs to flow through many elements to reach the end of the line. Rather, the liquid can also take shortcuts through higher-level representations, where long stretches of the line are represented by few tube elements. This enables the liquid to reach the end of the line much more quickly – to the extent that there are stretches sufficiently isolated from the distractors for coarse-scale representation at higher levels of the hierarchy.
Since the information about (1) the presence of oriented line segments, (2) their compatibility according to the Gestalt principle of good continuation, and (3) the attentional label are all available in the cortical hierarchy, a growth-cone algorithm could be implemented without thalamocortical loops. However, Schmid and Neumann argue that the non-orientation-specific thalamic representation reduces the complexity of the circuit. Fewer connections are required by decomposing the question “Are there upregulated compatible signals in the neighborhood?” into two simpler questions: “Are there compatible signals in the neighborhood?” (answered by cortex) and “Are there upregulated signals in the neighborhood?” (answered by the thalamic input). Because there could be compatible signals in the neighborhood that are not upregulated, and upregulated signals that are not compatible, yeses to both questions of the decomposition do not in general imply a yes to the original question. However, if we assume that there is only one line segment per location, then two yeses do imply a yes to the original question.
Schmid and Neumann argue that thalamic label map enables a simpler circuit that works in the simulations presented, even tracing a line as it crosses another line without spillover. We wonder if, in addition to requiring fewer connections, the thalamic label map might have functional advantages in the context of a system that must be able to perform not just line tracing but many other binding tasks, where the thalamus might have the same role, but the priors defining compatibility could differ.
Why is this model important? Line tracing is a type of computational problem that is prototypical of vision and yet challenging for both of our favorite modes of thinking about visual computations: deep feedforward neural networks and probabilistic inference. These two approaches (discriminative and generative to a first approximation) form diametrically opposed corners in a vast space of visual algorithms that has only begun to be explored (Peters et al. pp2023). Line tracing is a simple example of a visual cognition task that can be rendered intractable for both approaches by making the line snaking its way through the clutter sufficiently long and the clutter sufficiently close and confusing. Feedforward deep neural networks have trouble with this kind of problem because there are no hints in the local texture revealing the long-range connectivity of the lines. The combinatorics creates too rich a space of possible curves to represent with a hierarchy of features in a neural network. Although any recurrent computation (including the model of Schmid and Neumann and a recent line tracing model from Linsley & Serre, 2019) can be unfolded into a feedforward computational graph, the feedforward network would have to be very deep, and its parameters might be hard to learn without the inductive bias that iterating the same local propagation rule is the solution to the puzzle (van Bergen & Kriegeskorte 2020). From a probabilistic inference perspective, similarly, the problem is likely intractable in its general form because of the exponential number of possible groupings we would need to compute a posterior distribution over.
By assuming that we can be certain about the way things connect locally, we can avoid having to maintain a probability distribution over all possible line continuations from the fixation point. Binarizing the probabilities turns the problem into a region growing (or graph search) problem requiring a sequential procedure, because later steps depend on the result of earlier steps.
Schmid and Neumann’s paper describes how the previously proposed growth-cone algorithm, which solves an important computational challenge at the heart of visual cognition (Roelfsema 2006), might be implemented in the primate brain. The paper seriously engages both the neuroscience (at least at a qualitative level) and the computational problem, and it connects the two. The authors simulate the model and demonstrate its predictions of the key behavioral and neurophysiological results from the literature. They use model-ablation experiments to establish the necessity of different components. They also describe the model at a more abstract level: reducing the operations to sequential logical operations and systematically considering different possible implementations in a circuit and their costs in terms of connections. This resource-cost perspective deepens our understanding of the algorithm and reveals that the proposed model is attractive not only for its consistency with neuroanatomical, neurophysiological, and behavioral data, but also for the efficiency of implementation in a physical network.
Strengths
- Offers a candidate explanation for how an important cognitive function might be implemented in the primate brain, using an algorithm that combines parallel computation, hierarchical abstraction, and sequential inference.
- Motivated by a large body of experimental evidence from neurophysiological and behavioral experiments, the model is consistent with primate neuroanatomy, neural connectivity, neurophysiology, and subcellular dynamics in multi-compartment pyramidal neurons.
- Describes a class of related algorithms and network implementations at an abstract level, providing a deeper understanding of alternative possible neural mechanisms that could perform this cognitive function and their network complexity.
Weaknesses
- The model operates on a toy version of the task, using abstracted stimuli with few orientations and predefined Gabor filter banks as model representations, rather than more general visual representations learned from natural images. An important question is to what extent the algorithm will be able to perform visual tasks on natural images. Given the complexity of the paper as is, this question should be considered beyond the scope, but related work connecting these ideas to computer vision could be discussed in more detail.
Major suggestions
(1) Illustrate the computational mechanism and operation of the model more intuitively. In Fig. 1b, colors code for the level of representations. It would therefore be better to not use green to code for the selection tag. Thicker black contours or some other non-color marker could be used. It is also hard to see that the no-interference and the interference cases have different stimuli. Only the bottom panels with the stimuli show a slight difference. The top panels should be distinct as well since different neurons would be driven by the two stimuli. Alternatively, you could consider using only one stimulus, where the distractor distance variation is quite pronounced, but showing time frames to illustrate the variation of the speed of the progression of attentional tagging.
(2) Discuss challenges in scaling and calibrating the model for application to natural continuous curves. The stimuli analyzed have only a few orientations with sudden transitions from one to the other. Would the model as implemented also work for continuous curves such as those used in the neurophysiological and behavioral experiments or would a finer tiling of orientations be required? Under what conditions would attention spill over to nearby distractor curves? It would be good to elaborate on the roles of surround suppression, inhibition among detectors, and the excitation/inhibition balance.
(3) Discuss challenges in scaling the model to computer vision tasks on natural images. To be viable as brain-computational theories, models ultimately need to scale to natural tasks. Please address the challenges of extending the model for application to natural images and computer-vision tasks. This will likely require the representations to be learned through backpropagation. The cited complementary work by Linsley and Serre on the pathfinder task using horizontal gated recurrent units and incremental segmentation for computer vision is relevant here and deserves to be elaborated on in the Discussion. In particular, do the growth-cone model and your modeling results suggest an alternative neural network architecture for learning incremental binding operations?
Minor suggestions
(1) Please make sure that the methods section contains all the details of the model architecture needed for replication of the work. Much of the math is described well. But some additional technical details on maps and connectivity may be needed. What are the sizes of the maps? What do they look like for a given input? Do they appear like association fields? What is the excitatory and inhibitory connectivity as a function of spatial locations and orientations of the source and target unit?
(2) Discuss how the model relates to the results of Chen et al. (2014) who described the interplay between V1 and V4 during incremental contour integration on the basis of simultaneous recordings in monkeys.
(3) Although the paper is well-written and clear, the English is a bit rocky throughout with many grammatical errors and some typos. These could be fixed using a proofreader or suitable software.
– Nikolaus Kriegeskorte & Hossein Adeli
References
Chen M, Yan Y, Gong X, Gilbert CD, Liang H, Li W (2014) Incremental integration of global contours through interplay between visual cortical areas Neuron.
Halassa MM, Kastner S. Thalamic functions in distributed cognitive control. Nature neuroscience. 2017 Dec;20(12):1669-79.
Lamme VA, Roelfsema PR (2000) The distinct modes of vision offered by feedforward and recurrent processing Trends in Neurosciences.
Larkum M. A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends in neurosciences. 2013 Mar 1;36(3):141-51.
Larkum ME, Zhu JJ, Sakmann B (1998) A new cellular mechanism for coupling inputs arriving at different cortical layers Nature.
Linsley D, Kim J, Veerabadran V, Serre T (2019) Learning long-range spatial dependencies with horizontal gated-recurrent units NeurIPS. arxiv.org/abs/1805.08315.
Peters B, Kriegeskorte N (2021) Capturing the objects of vision with neural networks. Nature human behaviour Nature Human Behavior.
Peters B, DiCarlo JJ, Gureckis T, Haefner R, Isik L, Tenenbaum J, Konkle T, Naselaris T, Stachenfeld K, Tavares Z, Tsao D, Yildirim I, Kriegeskorte N (under review) How does the primate brain combine generative and discriminative computations in vision? CCN GAC paper. arXiv preprint arXiv:2401.06005.
Pooresmaeili A, Roelfsema PR (2014) A growth-cone model for the spread of object-based attention during contour grouping Current Biology.
Roelfsema PR, Lamme VA, Spekreijse H (1998) Object-based attention in the primary visual cortex of the macaque monkey Nature.
Roelfsema PR (2006) Cortical algorithms for perceptual grouping Annu Rev Neurosci.
Scholl BJ (2007) Object persistence in philosophy and psychology Mind & Language.
van Bergen RS, Kriegeskorte N (2020) Going in circles is the way forward: the role of recurrence in visual inference Current Opinion in Neurobiology.


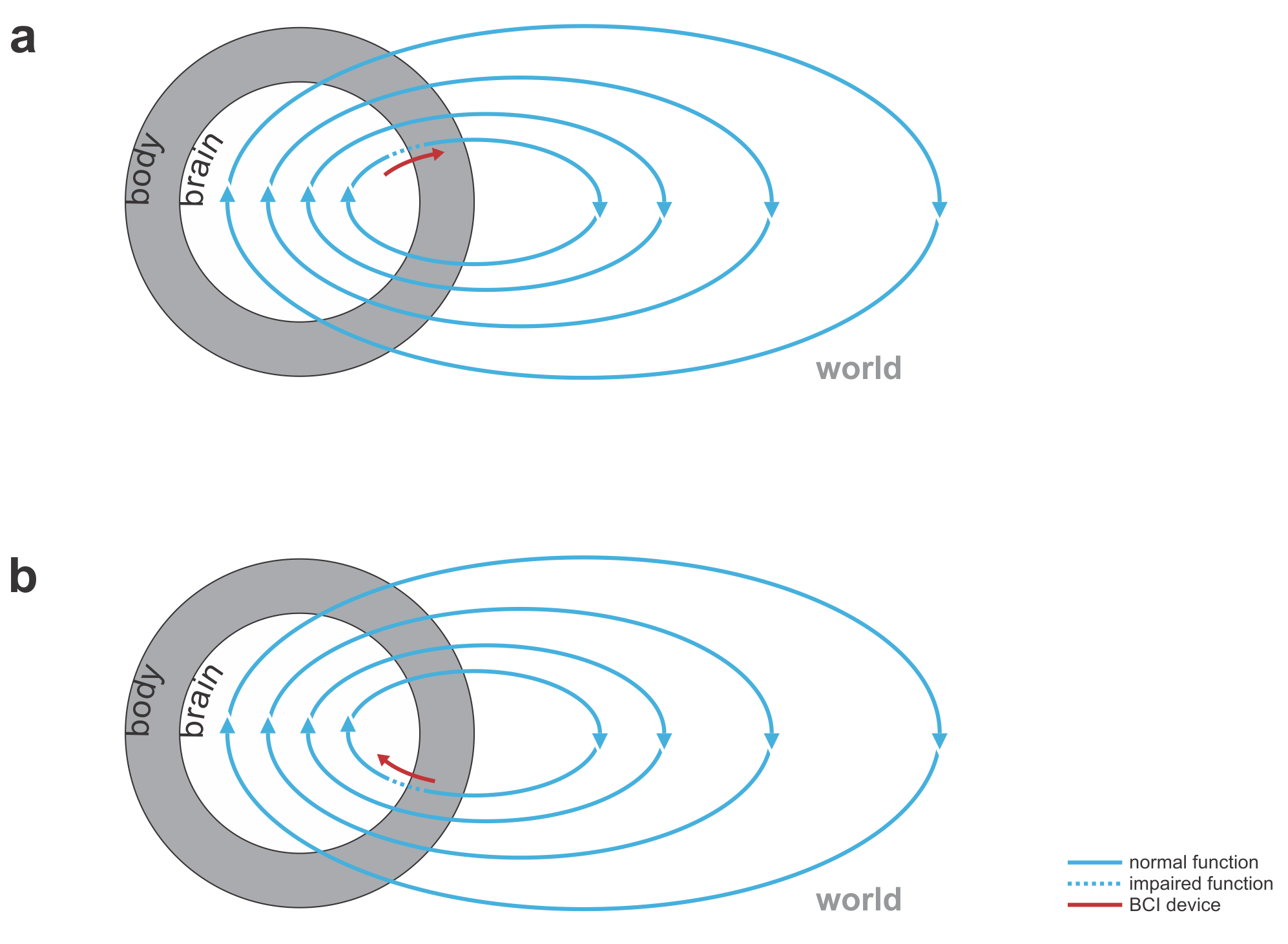
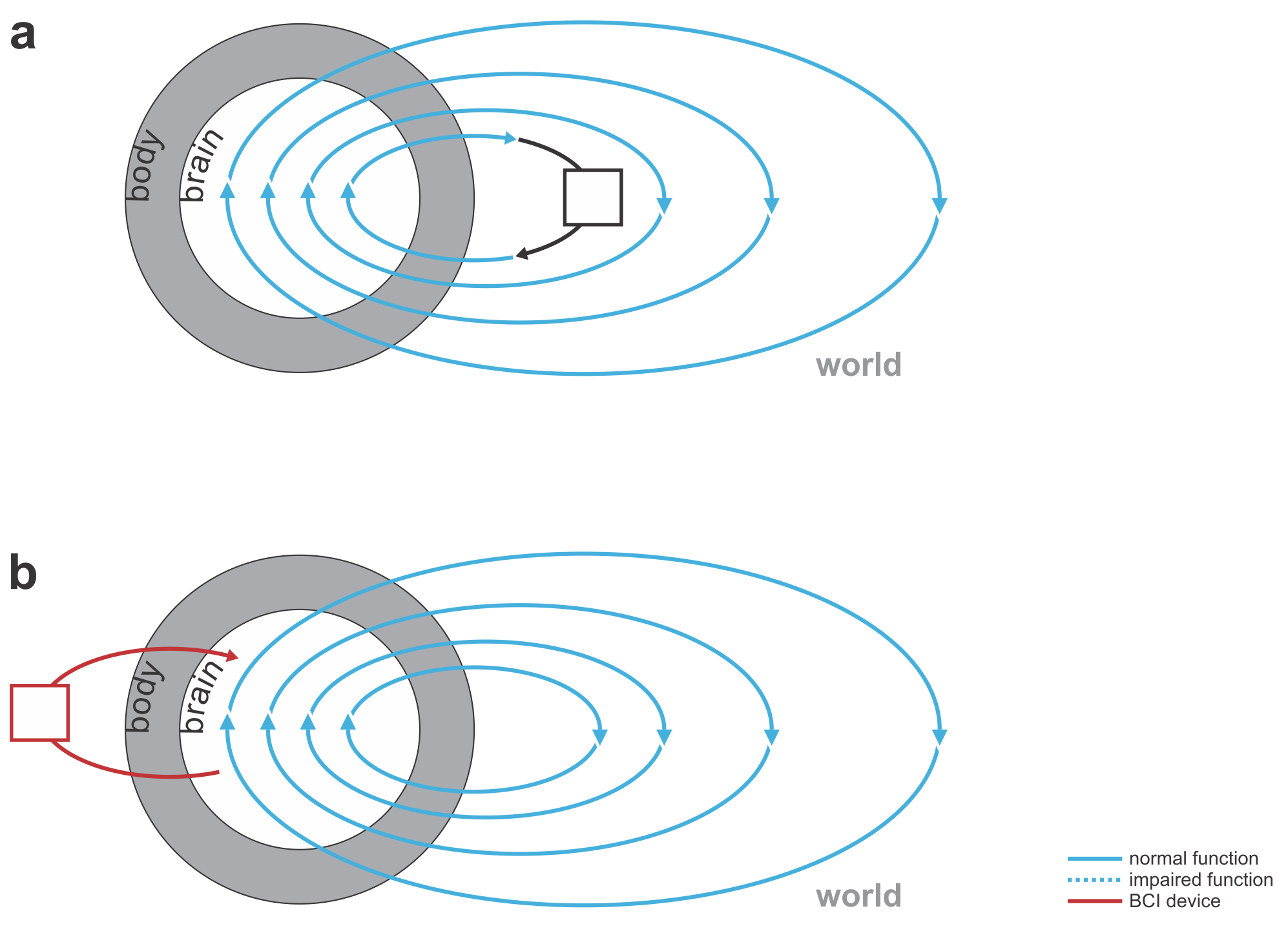
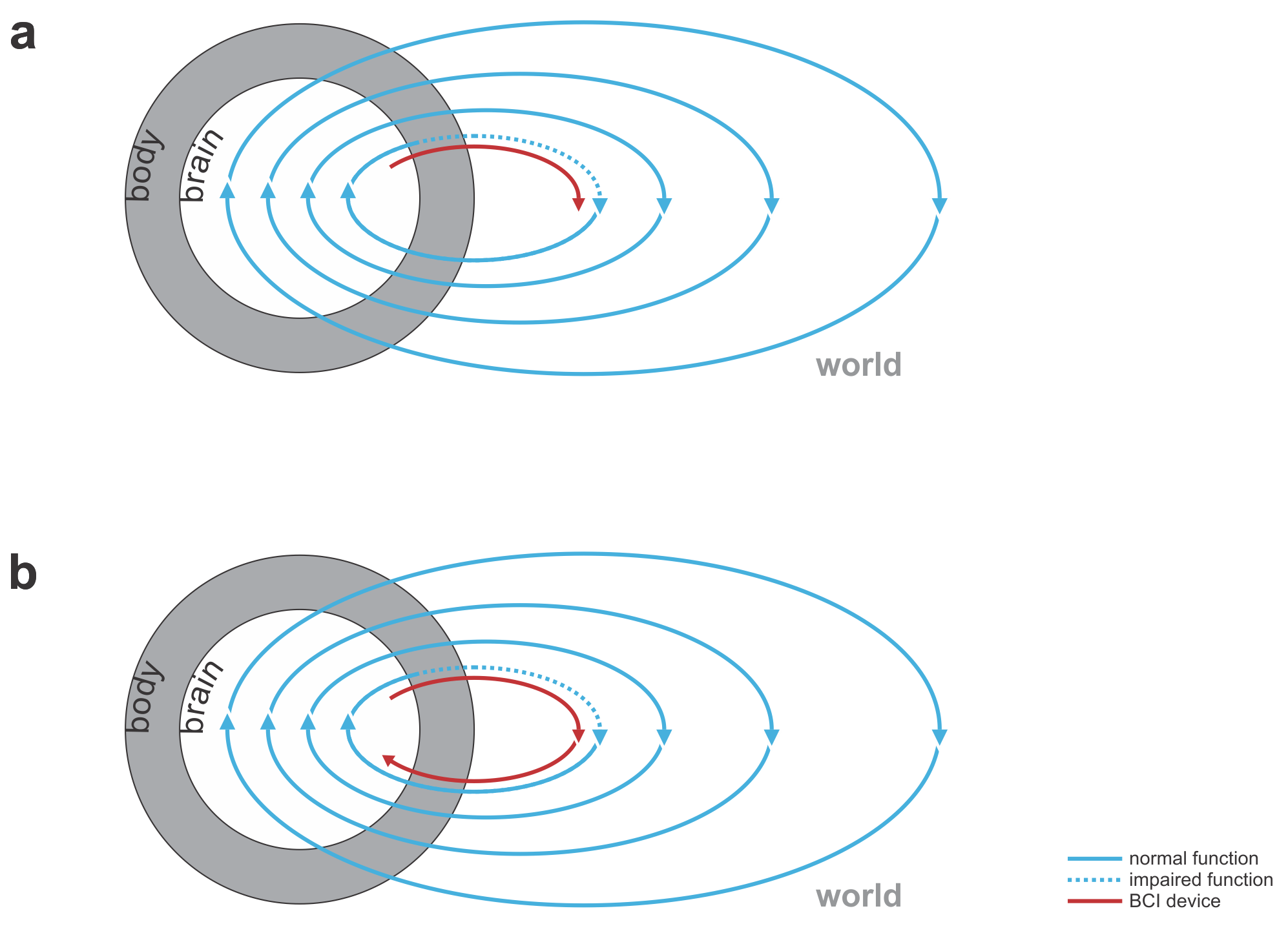 Fig. 1 | Uni- and bidirectional prosthetic-control BCIs. (a) A unidirectional BCI (red) for control of a prosthetic hand that reads out neural signals from motor cortex. The patient controls the hand using visual feedback (blue arrow). (b) A bidirectional BCI (red) for control of a prosthetic hand that reads out neural signals from motor cortex and feeds back tactile sensory signals acquired through artificial sensors to somatosensory cortex.
Fig. 1 | Uni- and bidirectional prosthetic-control BCIs. (a) A unidirectional BCI (red) for control of a prosthetic hand that reads out neural signals from motor cortex. The patient controls the hand using visual feedback (blue arrow). (b) A bidirectional BCI (red) for control of a prosthetic hand that reads out neural signals from motor cortex and feeds back tactile sensory signals acquired through artificial sensors to somatosensory cortex.