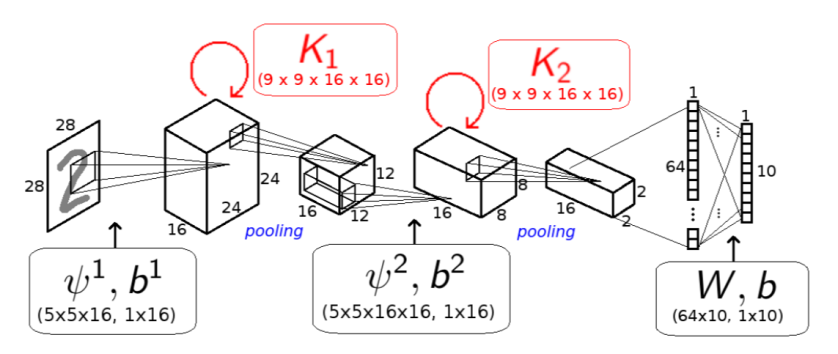
[I7R7]
Montobbio, Bonnasse-Gahot, Citti, & Sarti (pp2019) present an interesting model of lateral connectivity and its computational function in early visual areas. Lateral connections emanating from each unit drive other units to the degree that they are similar in their receptive profiles. Two units are symmetrically laterally connected if they respond to stimuli in the same region of the visual field with similar selectivity.
More precisely, lateral connectivity in this model implements a diffusion process in a space defined by the similarity of bottom-up filter templates. The similarity of the filters is measured by the inner product of the filter weights. Two filters that do not spatially overlap, thus, are not similar. Two filters are similar to the extent that their filters don’t merely overlap, but have correlated weight templates. Connecting units in proportion to their filter similarity results in a connectivity matrix that defines the paths of diffusion. The diffusion amounts to a multiplication with a convolution matrix. It is the activations (after the ReLU nonlinearity) that form the basis of the linear diffusion process.
The idea is that the lateral connections implement a diffusive spreading of activation among units with similar filters during perceptual inference. The intuitive motivation is that the spreading activation fills in missing information or regularizes the representation. This might make the representation of an image compromised by noise or distortion more like the representation of its uncompromised counterpart.
Instead of performing n iterations of the lateral diffusion at inference, we can equivalently take the convolutional matrix to the n-th power. The recurrent convolutional model is thus equivalent to a feedforward model with the diffusion matrix multiplication inserted after each layer.
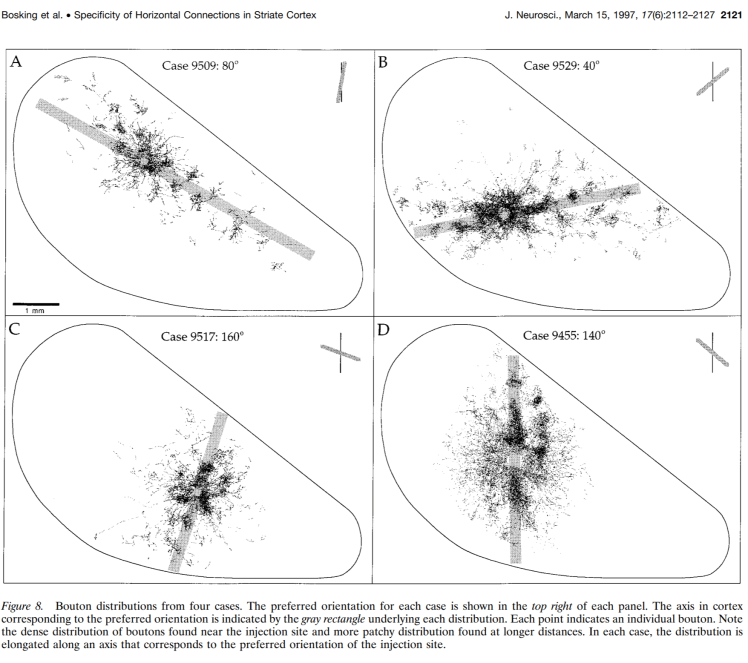
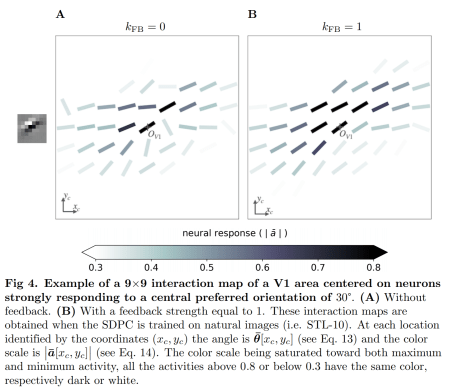
In the context of Gabor-like orientation-selective filters, the proposed formula for connectivity results in an anisotropic kernel of lateral connectivity that looks plausible in that it connects approximately collinear edge filters. This is broadly consistent with anatomical studies showing that V1 neurons selective for oriented edges form long-range (>0.5 mm in tree shrew cortex) horizontal connections that preferentially target neurons selective for collinear oriented edges.
Since the similarity between filters is defined in terms of the bottom-up filter templates, it can be computed for arbitrary filters, e.g. filters learned through task training. The lateral connectivity kernel for each filter, thus, does not have to be learned through experience. Adding this type of recurrent lateral connectivity to a convolutional neural network (CNN), thus, does not increase the parameter count.
The authors argue that the proposed connectivity makes CNNs more robust to local perturbations of the image. They tested 2-layer CNNs on MNIST, Kuzushiji-MNIST, Fashion-MNIST, and CIFAR-10. They present evidence that the local anisotropic diffusion of activity improves robustness to noise, occlusions, and adversarial perturbations.
Overall, the authors took inspiration from visual psychophysics (Field et al. 1992; Geisler et al. 2001) and neurobiology (Bosking et al. 1997), abstracted a parsimonious mathematical model of lateral connectivity, and assessed the computational benefits of the model in the context of CNNs that perform visual recognition tasks. The proposed diffusive lateral activation might not be the whole story of lateral and recurrent connectivity in the brain, but it might be part of the story. The idea deserves careful consideration.
The paper is well written and engaging. I’m left with many questions as detailed below. In case the authors chose to revise the paper, it would be great to see some of the questions addressed, a deeper exploration of the functional mechanism underlying the benefits, and some more challenging tests of performance.

Questions and thoughts
1 Can the increase in robustness be attributed to trivial forms of contextual integration?
If the filters were isotropic Gaussian blobs, then the diffusion process would simply blur the image. Blurring can help reduce noise and might reduce susceptibility to adversarial perturbations (especially if the adversary is not enabled to take this into account). Image blurring could be considered the layer-0 version of the proposed model. What is its effect on performance?
Consider another simplified scenario: If the network were linear, then the lateral connectivity would modify the effective filters, but each filter would still be a linear combination of the input. The model with lateral connectivity could thus be replaced by an equivalent feedforward model with larger kernels. Larger kernels might yield responses that are more robust to noise. Here the activation function is nonlinear, but the benefits might work similarly. It would be good to assess whether larger kernels in a feedforward network bring similar benefits to generalization performance.
2 Were the adversarial perturbations targeted at the tested model?
Robustness to adversarial attack should be tested using adversarial examples targeting each particular model with a given combination of numbers of iterations of lateral diffusion in layers 1 and 2. Was this the case?
3 Is the lateral diffusion process invertible?
The lateral diffusion is a linear transform that maps to a space of equal dimension (like Gaussian blurring of an image).
If the transform were invertible, then it would constitute the simplest possible change (linear, information preserving) to the representational geometry (as characterized by the Euclidean representational distance matrix for a set of stimuli). To better understand why this transform helps, then, it would be interesting to investigate how it changes the representational geometry for a suitable set of stimuli.
If lateral diffusion were not invertible, then it is perhaps best thought of as an intelligent type of pooling (despite the output dimension being equal to the input dimension).
4 Do the lateral connections make representations of corrupted images more similar to representations of uncorrupted versions of the same images?
The authors offer an intuitive explanation of the benefits to performance: Lateral diffusion restores the missing parts or repairs what has been corrupted (presumably using accurate prior information about the distribution of natural images). One could directly assess whether this is the case by assessing whether lateral diffusion moves the representation of a corrupted image closer to the representation of its uncorrupted variant.
5 Do correlated filter templates imply correlated filter responses under natural stimulation?
Learned filters reflect features that occur in the training images. If each image is composed of a mosaic of overlapping features, it is intuitive that filters whose templates overlap and are correlated will tend to co-occur and hence yield correlated responses across natural images. The authors seem to assume that this is true. But is there a way to prove that the correlations between filter templates really imply correlation of the filter outputs under natural stimulation? For independent noise images, filters with correlated templates will surely produce correlated outputs. However, it’s easy to imagine stimuli for which filters with correlated templates yield uncorrelated or anticorrelated outputs.
6 Does lateral connectivity reflecting the correlational structure of filter responses under natural stimulation work even better than the proposed approach?
Would the performance gains be larger or smaller if lateral connectivity were determined by filter-output correlation under natural stimulation, rather than by filter-template similarity?
Is filter-template similarity just a useful approximation to filter-output correlation under natural stimulation, or is there a more fundamental computational motivation for using it?
7 How does the proposed lateral connectivity compare to learned lateral connectivity when the number of connections (instead of the number of parameters) is matched?
It would be good to compare CNNs with lateral diffusive connectivity to recurrent convolutional neural networks (RCNNs) for matched sizes of bottom-up and lateral filters (and matched numbers of connections, not parameters). In addition, it would then be interesting to initialize the RCNNs with diffusive lateral connectivity according to the proposed model (after initial training without lateral connections). Lateral connections could precede (as in typical RCNNs) or follow (as in KerCNNs) the nonlinear activation function.
8 Does the proposed mechanism have a motivation in terms of a normative model of visual inference?
Can the intuition that lateral connections implement shrinkage to a prior about natural image statistics be more explicitly justified?
If the filters serve to infer features of a linear generative model of the image, then features with correlated templates are anti-correlated given the image (competing to explain the same variance). This suggests that inhibitory connections are needed to implement the dynamics for inference. Cortex does rely on local inhibition. How does local inhibitory connectivity fit into the picture?
Can associative filling in and competitive explaining away be reconciled and combined?
Strengths
- A mathematical model of lateral connectivity, motivated by human visual contour integration and studies on V1 long-range lateral connectivity, is tested in terms of the computational benefits it brings in the context of CNNs that recognize images.
- The model is intuitive, elegant, and parsimonious in that it does not require learning of additional parameters.
- The paper presents initial evidence for improved generalization performance in the context of deep convolutional neural networks.
Weaknesses
- The computational benefits of the proposed lateral connectivity is tested only in the context of toy tasks and two-layer neural networks.
- Some trivial explanations for the performance benefits have not been ruled out yet.
- It’s unclear how to choose the number of iterations of lateral diffusion for each of the the two layers, and choosing the best combination might positively bias the estimate of the gain in accuracy.

Minor point
“associated to” -> “associated with” (in several places)